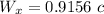Answer:
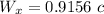
Step-by-step explanation:
given,
velocity of particle 1 = 0.741 c to left
velocity of second particle = 0.543 c to right
relative velocity between the particle = ?
for the relative velocity calculation we have formula
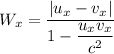
u_x = 0.543 c
v_x = - 0.741 c
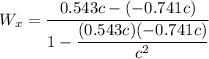
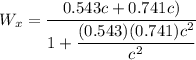
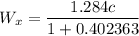
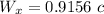
Relative velocity of the particle is