Question

A string that passes over a pulley has a 300 kg mass attached to one end and a 450 kg mass attached to the other end. The pulley, which is a disk of radius 10 cm, has friction in its axle. What is the magnitude of the frictional torque that must be exerted by the axle if the system is to be in static equilibrium?

Answer 1

Answer:147 N-m

Step-by-step explanation:

Given

mass of first Pulley
`m_1=300 kg`

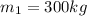
mass of second Pulley
`m_2=450 kg`

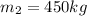
radius of Pulley
`r=10 cm`

If the system is in equilibrium then tension in the
`m_1` side mass is

`T_1=m_1g`

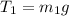
Tension in
`m_2` side block

`T_2=m_2g`

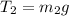
Net torque is

`\tau =(T_2-T_1)* r`

`\tau =(m_2-m_1)g* r`

`\tau =(450-300)* 9.8* 0.1`

`\tau =147 N-m`

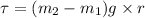
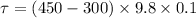
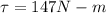
therefore Frictional Force must apply a force of 147 N-m in order to system remains in equilibrium