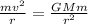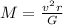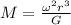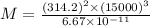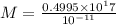Question

Certain neutron stars (extremely dense stars) are believed to be rotating at about 50 rev/s. If such a star has a radius of 15 km, what must be its minimum mass so that material on its surface remains in place during the rapid rotation?

Answer 1

Answer:
`M=49.95* 10^(26) kg`

Step-by-step explanation:

Given

`N=50 rev/s`

`\omega =2\pi N`

`\omega =2\pi \cdot 50=314.2 rad/s`

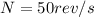
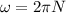
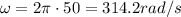
radius of neutron star
`r=15 km`

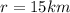
Centripetal force on material having mass m is given by

`F_c=(mv^2)/(r)`

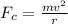
Gravitational Force between neutron star and mass m is

`F_g=(GMm)/(r^2)` ,where M=mass of Neutron star

equating centripetal Force and Gravitational Pull

`(mv^2)/(r)=(GMm)/(r^2)`

`M=(v^2r)/(G)`

`M=(\omega ^2r^3)/(G)`

`M=((314.2)^2* (15000)^3)/(6.67* 10^(-11))`

`M=(0.4995* 10^17)/(10^(-11))`

`M=49.95* 10^(26) kg`