Question

A company with a fleet of 150 cars found that the emissions systems of only 5 out of the 22 they tested failed to meet pollution control guidelines. The company initially believed that 20% of the fleet was out of compliance. Is this strong evidence the percentage of the fleet out of compliance is different from their initial thought? Your Question: State the null hypothesis and the alternative hypotheses they should use for completing a hypothesis test.

Answer 1

Answer: No, the percentage of the fleet out of compliance is not different from their initial thought.

Explanation:

Since we have given that

n = 22

x = 5

So,
`\hat{p}=(x)/(n)=(5)/(22)=0.23`

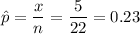
he company initially believed that 20% of the fleet was out of compliance. Is this strong evidence the percentage of the fleet out of compliance is different from their initial thought.

so, p = 0.2

Hypothesis would be

`H_0:p=\hat{p}\\\\H_a:p\\eq \hat{p}`

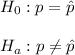
So, the t test statistic value would be

`t=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}\\\\\\t=\frac{0.23-0.20}{\sqrt{(0.2* 0.8)/(22)}}\\\\\\t=(0.03)/(0.085)\\\\t=0.353`

Degree of freedom = df = n-1 = 22-1 =23

So, t{critical value} = 2.080

So, 2.080>0.353

so, we will accept the null hypothesis.

Hence, No, the percentage of the fleet out of compliance is not different from their initial thought.