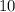Question

If the length of one side of a square is triple and the length of an adjacent side is increased by 10, the resulting rectangle has an area that is 6 times the area of the original square. Find the length of a side pf the original square.

Answer 1

10

Explanation:

Given: If the length of one side of a square is triple and the length of an adjacent side is increased by
`10`.

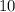To Find: If area is
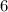`6` times the area of original square find length of a side of original square.

Solution:

Let the side of original square be
`=\text{x}`

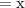
area of original square
`=\text{x}^2`

when length of side is tripled,

new length of one side of square
`=3\text{x}`

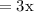
length of other side is increased by 10 unit

new length of other side of square
`=\text{x}+10`

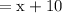
new area of resulting rectangle
`=\text{length of one side}*\text{length of other side}`

`=(\text{x}+10)*(3\text{x})`

`3\text{x}^(2)+30`

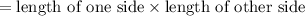
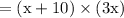
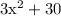
As area of resulting rectangle is 6 times the original square

`3\text{x}^(2)+30=6\text{x}^2`

`3\text{x}^2-30=0`

`3\text{x}(\text{x}-10)=0`

`\text{x}=10,0`

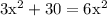
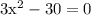
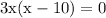
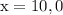
as length cannot be zero

`\text{x}=10`

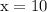
Hence the length of a side of original square is
`10`