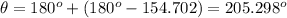Question

Cos(theta)= -.9041, 180degress< theta <270degress

Answer 1

`\theta=205.298^o`

Explanation:

We know

`cos\theta=-.9041`

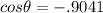
in the third quadrant
`180^o<\theta<270^o`

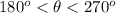
We use a scientific calculator to find the inverse cosine of -0.9041 to find

`\theta=154.702^o`

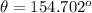
Since this angle is not in the required quadrant we must find the other angle who has the same cosine. The required angle is equidistant from the found value from the 180 degrees angle, so our solution is

`\theta=180^o+(180^o-154.702)=205.298^o`