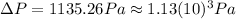Question

What must be the pressure difference between the two ends of a 2.6 km section of pipe, 36 cm in diameter, if it is to transport oil (rho = 950 kg/m^3, η = 0.20 Pa*s) at a rate of 900 cm^3/s ? Express your answer to two significant figures and include the appropriate units. Δ P = 1.3 x 10^3Pa

Answer 1

Answer:
`1.13(10)^(3) Pa`

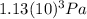
Step-by-step explanation:

This problem can be solved by the following equation:

`\Delta P=(8 \eta L Q)/(\pi r^(4))`

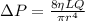
Where:

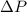`\Delta P` is the pressure difference between the two ends of the pipe

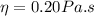`\eta=0.20 Pa.s` is the viscosity of oil

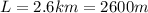`L=2.6 km=2600 m` is the length of the pipe

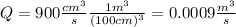`Q=900 (cm^(3))/(s) (1 m^(3))/((100 cm)^(3))=0.0009 (m^(3))/(s)` is the Rate of flow of the fluid

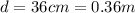`d=36 cm=0.36 m` is the diameter of the pipe

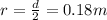`r=(d)/(2)=0.18 m` is the radius of the pipe

Soving for
`\Delta P`:

`\Delta P=(8 (0.20 Pa.s)(2600 m)(0.0009 (m^(3))/(s)))/(\pi (0.18 m)^(4))`

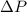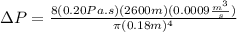
Finally:

`\Delta P=1135.26 Pa \approx 1.13(10)^(3) Pa`