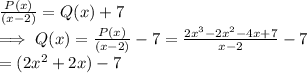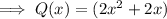Question

Using the remainder theorem to find p(2) for p(x)=2x^3-2x^2-4x+7

Give the quotient and the remainder for the associated division and the value of p(2)

Answer 1

In the given polynomial p(x)
`Q(x)  = (2x^2 + 2x)`

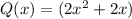
Remainder = p(2) = 7

Explanation:

Here, the given polynomial is
`p(x)=2x^3-2x^2-4x+7`

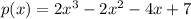
Also, p (2) is to be determined,

⇒ x = 2 is the zero of the given p(x)

⇒ (x- 2) is he Root of the polynomial.

Now, by REMAINDER THEOREM:

The remainder theorem states that when a polynomial, f(x), is divided by a linear polynomial , x - a, the remainder of that division will be equivalent to f(a).

So, here when p(x) is divided by ( x- 2) the remainder = p(2)

`(P(x))/((x-2))   = Q(x)  + p(2)`

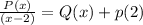
Now,
`p(2) =2(2)^3-2(2)^2-4(2)+7  =16 -8-8+7 = 7`

⇒ p(2) = 7

Now, the given equation becomes:

Now,
`(P(x))/((x-2))   = Q(x)  + 7\\\implies Q(x) =  (P(x))/((x-2))  - 7 =  (2x^3-2x^2-4x+7)/(x-2)  -7\\= (2x^2 + 2x)  - 7`

`\implies Q(x)  = (2x^2 + 2x)`