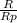Question

Gravitational Acceleration inside a Planet

Consider a spherical planet of uniform density rho. The distance from the planet's center to its surface (i.e., the planet's radius) is Rp. An object is located a distance R from the center of the planet, where R
Part A
Find an expression for the magnitude of the acceleration due to gravity, g(R), inside the planet.
Express the acceleration due to gravity in terms of rho, R, π, and G, the universal gravitational constant.

Part B
Rewrite your result for g(R) in terms of gp, the gravitational acceleration at the surface of the planet, times a function of R.
Express your answer in terms of gp, R, and Rp.

Answer 1

g(R) = gpR/Rp (both p are subscript)

Step-by-step explanation:

Notice that g

increases linearly with R

, rather than being proportional to 1/R^2

. This assures that it is zero at the center of the planet, as required by symmetry.

Answer 2

PART A

g(R) =
`(G(rho)(4)\pi R)/(3)` ;

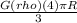PART B

g(R) = g(Rp) ×
`(R)/(Rp)`.

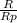Step-by-step explanation:

Given density of planet = rho.

The planet's radius = Rp.

An object is located a distance R from the center of the planet,

where R< Rp.

The gravitational fore between two point masses m₁ and m₂ is,

F =
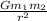`(Gm_(1)m_(2))/(r^(2) )` ; G= universal gravitational constant

r = distance between the masses.

for mass m₂ , F= m₂ g; where g = acceleration due to gravity;

so, g =
`(F)/(m_(2) )` =
`(Gm_(1))/(r^(2) )`;

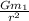From figure, only inside part of the planet exerts force and which can be treated as a point mass.

so, g =
`(Gm_(R))/(R^(2) )`

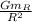
where
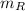`m_(R)` = mass of the planet with radius R.

⇒
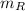`m_(R)` = rho ×
`(4)/(3)`
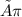`×\pi`×R³

⇒ g(R) =
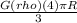`(G(rho)(4)\pi R)/(3)` → PART A

PART B

At the surface g(Rp) =
`(G(rho)(4)\pi Rp)/(3)`

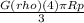
⇒ g(R) = g(Rp) ×
`(R)/(Rp)`