Question

A person at the equator on the surface of the earth is standing on a scale. The mass of the person is 80 kg. The radius of the earth is 6.38x10^6 m.

1. What is the period of the earth rotation in seconds?

2. What is the velocity of the person on the equator?

Answer 1

The "period of rotation of the earth" in seconds is 86164.09053 seconds.

"Velocity of the person on the equator" is 2.89
`2.8* 10^(-8) \mathrm{m} / \mathrm{s}^(2)`.

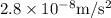Step-by-step explanation:

(1) The earth rotates once every 23 hours, 56 minutes and 4.09053 seconds,

Reason: The "earth" is the "third planet" from "the sun". For every one the "period of rotation of the earth" is 24 hours, but the actual value is "23 hours" "56 minutes" and "4 seconds". This happens because a "solar day" is "longer" than a "sidereal day". The "period of rotation of earth" in seconds is 23 hours × 3600 seconds + 56 minutes × 60 + 4.09053 seconds = 86164.09053 seconds

The "period of rotation of the earth in seconds" is 86164.09053 seconds.

(2) The velocity of the person on the equator:

`\mathrm{V}^(2)=(G M)/(R)`

`\text { Where, } G \text { is } 6.673 * 10^(-12) \mathrm{N} \bullet \mathrm{m}^(2) / \mathrm{kg}^(2)`

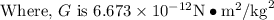
M is the mass of the person is 80 kg

`\mathrm{R} \text { is the radius of the earth } 6.38 * 10^(6) \mathrm{m}`

`V^(2)=(6.673 * 10^(-11) * 80)/(6.37 * 10^(6))`

`V^(2)=(5.3384 * 10^(-9))/(6.37 * 10^(6))`

`\mathrm{V}^(2)=8.380 * 10^(-16)`

`\mathrm{V}=\sqrt{83.80 * 10^(-16)}`

`\mathrm{V}=2.89 * 10^(-8) \mathrm{m} / \mathrm{s}^(2)`

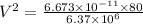
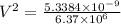
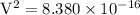
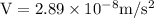
Velocity of the person on the equator is 2.89
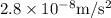`2.8* 10^(-8) \mathrm{m} / \mathrm{s}^(2)`.