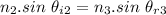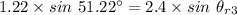Question

A flat uniform film with an index of refraction n2=1.22 is grown on top of a flat diamond. A light ray enters from the air above the film with an angle of incidence 72. What is the angle of refraction of the light ray once the ray has passed through the film layer and into the diamond?

Answer 1

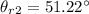`\theta_r_2=51.22^(\circ)` in the film medium

`\theta_r_3=23.34^(\circ)` in diamond medium

Step-by-step explanation:

Given:

• refractive index of film,
  `n_2=1.22`

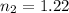
• angle of incident on the film from air,
  `\theta_i_1=72^(\circ)`

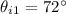
• We have refractive index of diamond,
  `n_3=2.4`

According to the Snell's Law:

`n_1.sin\theta_i_1=n_2.sin\theta_r_2`

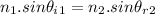
where:

`n_1=`refractive index of air ≈ 1

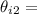`\theta_i_2=`is the angle of incident on the film in (medium 1) air

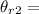`\theta_r_2=`is the angle of refraction in the (medium 2) film

Using Snell's law:

`1* sin72^(\circ)=1.22 * sin\theta_r_2^(\circ)`

`\theta_r_2=51.22^(\circ)`

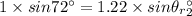
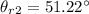
Now this angle will be the angle of incident for diamond.

`\theta_i_2=51.22^(\circ)`

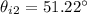
∴Angle of refraction in diamond medium after passing through film-diamond interface:

`n_2.sin\ \theta_i_2=n_3. sin\ \theta_r_3`

`1.22* sin\ 51.22^(\circ)=2.4* sin\ \theta_r_3`

`\theta_r_3=23.34^(\circ)`