Question

60,61,62,63 plzzz answer ​

Answer 1

Part 60) see the explanation

Part 61)
`ST=18\ units`

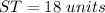
Part 62)
`x=5\ units`

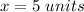
Part 63) The perimeter of triangle BDF is 81 units and the perimeter of triangle ACE is 162 units

Explanation:

Part 60) we know that

The AA Similarity Theorem states: If two angles of one triangle are congruent with two angles of another triangle, then the triangles are similar

In this problem

m∠DAE≅m∠BAC ----> is the same angle

m∠DEA≅m∠BCA ----> by corresponding angles

so

Two angles of triangle ADE are congruent with two angles of triangle ABC

therefore

Triangles ADE and ABC are similar by AA Similarity Theorem

Part 61) we know that

Triangles SXY and SUT are similar by AA Similarity Theorem

Remember that

If two figures are similar, then the ratio of its corresponding sides is proportional and its corresponding angles are congruent

`(SX)/(SU)=(SY)/(ST)`

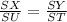
substitute the given values

`(5)/(9)=(10)/(ST)`

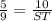
solve for ST

`ST=9(10)/5`

`ST=18\ units`

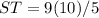
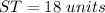
Part 62) we know that

Triangles of the figure are similar by AA Similarity Theorem

Remember that

If two figures are similar, then the ratio of its corresponding sides is proportional and its corresponding angles are congruent

`(x)/(x+(x+5))=(x-2)/((x-2)+(x+1))`

`(x)/(2x+5)=(x-2)/(2x-1)`

`x(2x-1)=(x-2)(2x+5)\\\\2x^(2) -x=2x^(2) +5x-4x-10\\\\2x^(2) -x=2x^(2)+x-10\\\\2x=10\\\\x=5\ units`

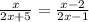
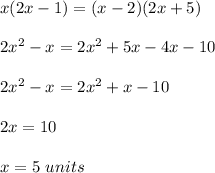
Part 63) we know that

The Midpoint Theorem states that the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side

Part a) Find the perimeter of triangle BDF

In this problem applying the Midpoint Theorem

`FB=(EC)/(2)`

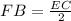
we have

`EC=50\ units`

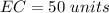
substitute

`FB=(50)/(2)=25\ units`

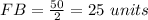
The perimeter of triangle BDF is equal to

`P=FB+BD+DF`

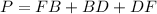
we have

`FB=25\ units`

`BD=35\ units`

`DF=21\ units`

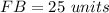
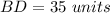
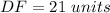
substitute

`P=25+35+21=81\ units`

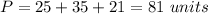
Part b) Find the perimeter of triangle ACE

In this problem applying the Midpoint Theorem

`EC=2FB`

`AC=2DF`

`AE=2BD`

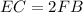
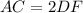
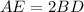
we have

`EC=50\ units`

`BD=35\ units`

`DF=21\ units`

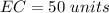
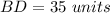
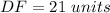
substitute

`AC=2(21)=42\ units`

`AE=2(35)=70\ units`

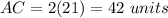
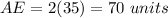
The perimeter of triangle ACE is equal to

`P=AC+EC+AE`

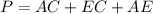
substitute the values

`P=42+50+70=162\ units`

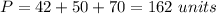
The perimeter of triangle ACE is two times the perimeter of triangle BDF