Question

A machine part has the shape of a solid uniform sphere of mass 245 g and diameter 4.30 cm . It is spinning about a frictionless axle through its center, but at one point on its equator it is scraping against metal, resulting in a friction force of 0.0200 N at that point. Find its angular acceleration. Let the direction the sphere is spinning be the positive sense of rotation.

Answer 1

Angular acceleration,
`\alpha =9.49\ rad/s^2`

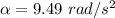
Step-by-step explanation:

It is given that,

Mass of the solid sphere, m = 245 g = 0.245 kg

Diameter of the sphere, d = 4.3 cm = 0.043 m

Radius, r = 0.0215 m

Force acting at a point, F = 0.02 N

Let
`\alpha` is its angular acceleration. The relation between the angular acceleration and the torque is given by :

`\tau=I* \alpha`

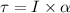
I is the moment of inertia of the solid sphere

For a solid sphere,
`I=(2)/(5)mr^2`

`\alpha =(\tau)/(I)`

`\alpha =(F.r)/((2/5)mr^2)`

`\alpha =(5F)/(2mr)`

`\alpha =(5* 0.02)/(2* 0.245* 0.0215)`

`\alpha =9.49\ rad/s^2`

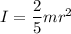
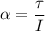
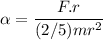
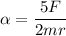
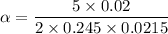
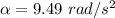
So, its angular acceleration is
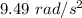`9.49\ rad/s^2`. Hence, this is the required solution.