Question

There are 1500 bees in a colony. Each month, the number of bees decreases by 12%. There are 800 flowering plants in a garden. Each month, 25 flowering plants are removed.

Part A: Write functions to represent the number of bees and the number of flowering plants throughout the months. (4 points)

Part B: How many bees are in the colony after 6 months? How many flowering plants are in the garden after the same number of months? (2 points)

Part C: After approximately how many months is the number of bees and the number of flowering plants the same? Justify your answer mathematically. (4 points)

(10 points)

Answer 1

n=6.77 months (exactly)

n=7 months (nearest integer, less accurate)

Explanation:

A) The initial number of bees in a colony is 1500. Each month the number of bees decreases by 12% which means each month we must factor by (1-0.12)=0.88

So the number of bees as a function of n months is

1500*0.88*0.88...0.88 (n times)

`B=1500*0.88^n`

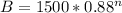
The initial number of flowering plants is 800 and there are 25 fewer of them each month. It can be written as

`P=800-25n`

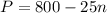
B) After 6 months (n=6) there will be

`B=1500*0.88^6\approx 697\ bees`

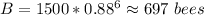
And there will be

`P=800-25(6)=650`flowering plants

C) We want to know the value of n that make B = P:

`1500*0.88^n=800-25n`

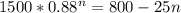
Rearranging

`1500*0.88^n-800+25n=0`

This equation cannot be solved by exact procedures, we must approach the answer or use any numerical method to solve for n

The best value to solve the equation is n = 6.77 months in which case

`B=1500*0.88^(6.77)\approx 631\ bees`

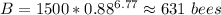
And
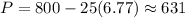`P=800-25(6.77)\approx 631` flowering plants

If we wanted to use only integers for n, then we should use the nearest integer to our previous value, that is, n=7. In this case,

`B=1500*0.88^7\approx 613\ bees`

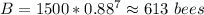
`P=800-25(7)= 625` flowering plants