Answer:
The values of x are -3 and 5
Explanation:
we have
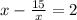
Multiply by x both sides to remove the fraction
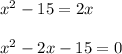
The formula to solve a quadratic equation of the form

is equal to

in this problem we have
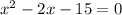
so
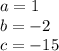
substitute in the formula
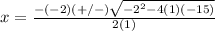
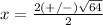
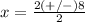
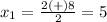
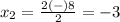
therefore
The values of x are -3 and 5