Question

A child twirls his yo-yo horizontally about his head rather than using it properly. The yo-yo has a mass of 0.200 kg and is attached to a string 0.800 m long. (a) If the yo-yo makes a complete revolution each second, what tension must exist in the string?

Answer 1

Tension in the string, F = 6.316 N

Step-by-step explanation:

It is given that,

Mass of the Yo - Yo, m = 0.2 kg

Length of the string, l = 0.8 m

It makes a complete revolution each second, angular velocity,
`\omega=2\pi\ rad`

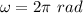
Let T is the tension exist in the string. The tension acting on it is equal to the centripetal force acting on it. Its expression is given by :

`F=(mv^2)/(r)`

`F=m\omega^2 r`

`F=0.2* (2\pi )^2 * 0.8`

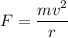
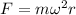
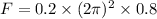
F = 6.316 N

So, the tension must exist in the string is 6.316 N. Hence, this is the required solution.