Question

The Aluminum Association reports that the average American uses 56.8 pounds of aluminum in a year. A random sample of 50 households is monitored for one year to determine aluminum usage. If the population standard deviation of annual usage is 12.1 pounds, what is the probability that the sample mean will be each of the following? Appendix A Statistical Tablesa. More than 58 poundsb. More than 57 poundsc. Between 55 and 57 poundsd. Less than 53 poundse. Less than 48 pounds

Answer 1

`\mu = 56.8`

`\sigma = 12.1`

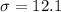
A)what is the probability that the sample mean will be More than 58 pounds

P(x>58)

Formula :
`Z=(x-\mu)/(\sigma)`

Substitute the values :

`Z=(58-56.8)/(12.1)`

`Z=0.09917`

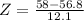
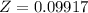
refer the z table

P(x<58)=0.5359

P(X>58)=1-P(x<58)=1-0.5359=0.4641

Hence the probability that the sample mean will be More than 58 pounds is 0.4641

B)what is the probability that the sample mean will be More than 57 pounds

P(x>57)

Formula :
`Z=(x-\mu)/(\sigma)`

Substitute the values :

`Z=(57-56.8)/(12.1)`

`Z=0.0165`

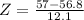
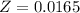
refer the z table

P(x<57)=0.5040

P(X>57)=1-P(x<57)=1-0.5040=0.496

Hence the probability that the sample mean will be More than 57 pounds is 0.496

C)what is the probability that the sample mean will be Between 55 and 57 pound

Formula :
`Z=(x-\mu)/(\sigma)`

Substitute the values :

`Z=(57-56.8)/(12.1)`

`Z=0.0165`

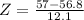
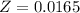
refer the z table

P(x<57)=0.5040

Formula :
`Z=(x-\mu)/(\sigma)`

Substitute the values :

`Z=(55-56.8)/(12.1)`

`Z=-0.1487`

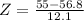
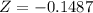
refer the z table

P(x<55)=0.4443

P(55<x<57)=P9x<57)-P(x<55) =0.5040-0.4443=0.0597

Hence the probability that the sample mean will be Between 55 and 57 pounds is 0.0597

D)what is the probability that the sample mean will be Less than 53 pounds

Formula :
`Z=(x-\mu)/(\sigma)`

Substitute the values :

`Z=(53-56.8)/(12.1)`

`Z=−0.314`

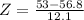
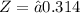
refer the z table

P(x<53)=0.3783

The probability that the sample mean will be Less than 53 pounds is 0.3783

E)what is the probability that the sample mean will be Less than 48 pounds

Formula :
`Z=(x-\mu)/(\sigma)`

Substitute the values :

`Z=(48-56.8)/(12.1)`

`Z=−0.727`

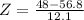
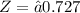
refer the z table

P(x<48)=0.2358

The probability that the sample mean will be Less than 48 pounds is 0.2358