Question

A 2.4-m high 200-m2 house is maintained at 22°C by an air-conditioning system whose COP, is 3.2. It is estimated that the kitchen, bath, and other ventilating fans of the house discharge a houseful of conditioned air once every hour. If the average outdoor temperature is 32°C, the density of air is 1.20 kg/m3, and the unit cost of electricity is $0.10/kWh, the amount of money "vented out" by the fans in 10 hours is

(a) $0.50
(b) $1.60
(c) $5.00
(d) $11.00
(e) $16.00

Answer 1

The amount that is "vented" out by "the fans" is $0.50 for 10 hours.

Option: a

Step-by-step explanation:

"Energy discharged by air in every hour" can be determined by,

`\mathrm{Q}=\mathrm{m}_{\mathrm{air}} \mathrm{C}_{\mathrm{p}} \Delta \mathrm{T}`

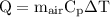
Q = heat energy (Joules, J)

m = mass of a substance (kg)

c = specific heat (units J/kg∙K)

`\mathrm{m}_{\mathrm{air}}=\rho \mathrm{v}`

`\text { Density of air } \rho=1.20 \mathrm{kg} / \mathrm{m}^(3)`

`\text { Density of air } \rho=1.20 * 200 * 2.4`

`\text { Density of air } \rho=576 \mathrm{kg}`

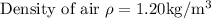
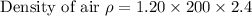
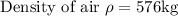
∆T = 10 hours

`\text { Specific Heat Capacities of Air. The nominal values used for air at } 300 \mathrm{K} \text { are } \mathrm{C_P}=1.00 \mathrm{kJ} / \mathrm{kg} . \mathrm{K}`

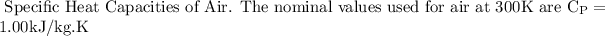
Q = 576 × 1.00 × 10

Q = 5760 kJ/hours

W = 1.6 kwh

We know that, “Coefficient of performance” (COP)

`\mathrm{Cop}=(Q)/(w)`

`\mathrm{W}=\frac{Q}{\mathrm{cop}}`

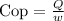
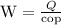
Given that, COP = 3.2

`\mathrm{W}=(1.6)/(3.2)`

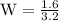
W = 0.5 kwh

The unit cost of electricity is $0.10/kWh

The unit cost of electricity is $0.10/kWh

Unit electricity cost for 10 hours = 0.5 × 10 × 0.1$

Unit electricity cost for 10 hours = $0.5

The amount that is "vented out" by "the fans" is $0.50 for 10 hours.