Question

The International Space Station orbits at an average height of 350 km above sea level.???? = 6.67× 10−11 ????m2 ????????2 ⁄ ????????????????????ℎ = 5.97 × 1024 ???????? ????????????????????ℎ = 6.37× 103 ????m(a) Determine the orbital speed of this space station.(b) The period of the space station.Draw it out for full credit

Answer 1

(a). The orbital speed of this space station is 7906.42 m/s.

(b). The period of the space station is 5062.2 sec.

Step-by-step explanation:

Given that,

Gravitational constant
`G=6.67*10^(-11)\ Nm^2/kg^2`

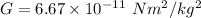
Mass of earth
`M_(e)=5.97*10^(24)\ kg`

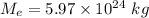
Radius of earth
`R_(e)=6.37*10^(3)\ km`

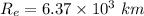
(a). We need to calculate the orbital speed of this space station

Using formula of orbital speed

`v=\sqrt{(GM)/(r)}`

`v=\sqrt{(6.67*10^(-11)*5.97*10^(24))/(6.37*10^(6))}`

`v=7906.42\ m/s`

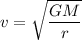
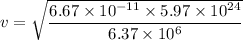
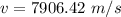
(b). We need to calculate the period of the space station

Using formula of period

`T=(2\pi r)/(v)`

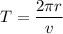
Put the value into the formula

`T=(2\pi*6.37*10^(6))/(7906.42)`

`T=5062.2\ sec`

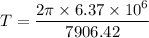
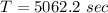
Hence, (a). The orbital speed of this space station is 7906.42 m/s.

(b). The period of the space station is 5062.2 sec.