Answer:
1.25 R
Step-by-step explanation:
Acceleration due to gravity on earth, ge = g
Acceleration due to gravity on planet, gP = 5 times the acceleration due to gravity on earth
gP = 5 g
Density of planet = 5 x density of earth
Let the radius of earth is R
Let the radius of planet is Rp.
Use the for acceleration due to gravity
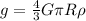
where, G s the universal gravitational constant and ρ be the density of planet.
For earth
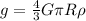 .... (1)
.... (1)
For planet
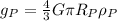
According to the question
gp = 5 g, ρP = 4 ρ
Substitute the values
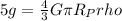 .... (2)
.... (2)
Divide equation (2) by equation (1), we get

Rp = 1.25 R
Thus, the radius of planet 1.25 R.