Answer:
Let x be the time taken( in minutes ) by younger gardener,
So, the one minute work of younger gardener =
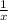
Also, the time taken by older gardener = (x+12) minutes ( given ),
So, the one minute work of older gardener =
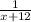
Total work done in one minute =
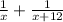
Now, total time taken = 8 minutes,
Total work done in one minute =
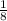
Thus,
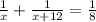
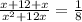
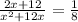
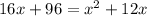
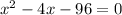
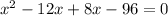
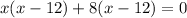
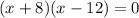
By zero product product property,
x + 8 =0 or x - 12 =0
⇒ x = -8 ( not possible ), x = 12
Hence, the time taken by younger gardener = 12 minutes,
And, the time taken by older gardener = 12 + 12 = 24 minutes.