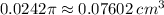Question

The volume of a spherical cancerous tumor is given by v(r)=4/3 p r^3 .

If the radius of a tumor is estimated at 1.1 cm, with a maximum error in measurement of 0.005 cm, determine the error that might occur when the volume of the tumor is calculated.

Answer 1

The error in the calculated volume is about
`0.0242\pi \approx 0.07602 \:cm^3`

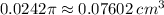
Explanation:

Given a function y=f(x) we call dy and dx differentials and the relationship between them is given by,

`dy=f'(x)dx`

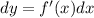
If the error in the measured value of the radius is denoted by
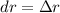`dr=\Delta r`, then the corresponding error in the calculated value of the volume is
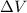`\Delta V`, which can be approximated by the differential

`dV=4\pi r^2dr`

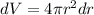
When r = 1.1 cm and dr = 0.005 cm, we get

`dV=4\pi (1.1)^2(0.005)=0.0242\pi`

The error in the calculated volume is about
`0.0242\pi \approx 0.07602 \:cm^3`