Question

Suppose a ball is thrown directly upward from a height of 7 feet with an initial velocity of 50 feet per second. Use the quadratic formula or a graphing calculator to find the number of seconds it takes the ball to hit the ground. Round the nearest tenth of a second.

Answer 1

t = 3.3 seconds

Explanation:

From the formula of vertical motion of an object under gravity we can write the equation

`H = ut + (1)/(2) gt^(2)` ....... (1)

Where u is the initial velocity (in feet per second) of throw of the object and t is time of travel in seconds and the value of g i.e. gravitational acceleration is 32 feet/sec².

Now, while a ball is thrown vertically upward with velocity 50 ft/sec from a height of 7 ft then the time of travel of the ball before reaching the ground, the equation (1) will be written as

`- 7 = 50t - (1)/(2) * 32 * t^(2)`

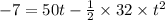
As we have selected the upward direction as positive so, gravitational acceleration,g will be negative and as the displacement is downward by 7 feet, so it will be negative.

⇒ 16t² - 50t - 7 = 0 ........ (2)

Now, applying Sridhar Acharya formula,

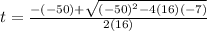`t = \frac{-(-50) + \sqrt{(-50)^(2) - 4(16)(-7)}}{2(16)}` {Neglecting the negative root as t can not be negative}

⇒ t = 3.3 seconds {Rounded to the nearest tenth}

(Answer)