Question

Jupiter's moon Io has active volcanoes (in fact, it is the most volcanically active body in the solar system) that eject material as high as 500 km (or even higher) above the surface. Io has a mass of 8.93×1022 kg and a radius of 1821 km . For this calculation, ignore any variation in gravity over the 500-km range of the debris.

Answer 1

The height reached by the material on Earth is 91 km.

Step-by-step explanation:

Given that,

Mass
`M_(Io)=8.93*10^(22)\ kg`

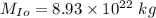
Radius = 1821 km

Height
`h_(Io)=500\ km`

Suppose we need to find that how high would this material go on earth if it were ejected with the same speed as on Io?

We need to calculate the acceleration due to gravity on Io

Using formula of gravity

`g =(GM_(Io))/((R_(Io))^2)`

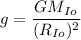
Put the value into the formula

`g=(6.67*10^(-11)*8.93*10^(22))/((1821*10^(3))^2)`

`g=1.79\ m/s^2`

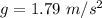
Let v be the speed at which the material is ejected.

We need to calculate the height

Using the formula of height

`H=(v^2)/(2g)`

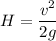
Using ratio of height of earth and height of Io

`(H_(e))/(H_(Io))=((v^2)/(2g_(e)))/((v^2)/(2g_(Io)))`

`(H_(e))/(H_(Io))=(g_(Io))/(g_(e))`

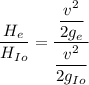
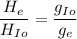
Put the value into the formula

`(H_(e))/(H_(Io))=(1.79)/(9.8)`

`(H_(e))/(H_(Io))=0.182`

`H_(e)=0.182* H_(Io)`

`H_(e)=0.182*500`

`H_(e)=91\ km`

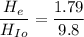
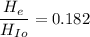
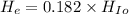
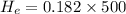
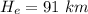
Hence, The height reached by the material on Earth is 91 km.