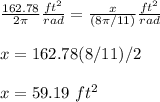Answer:
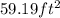
Explanation:
step 1
Find the area of the circle
The area of the circle is equal to
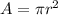
we have
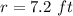
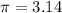
substitute
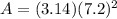
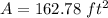
step 2
we know that
The area of a circle subtends a central angle of 2π radians
so
using proportion
Find out the area of a sector with a central angle of 8 π/11 radians