Question

Two rectangles have the same width. The length of one is 1 foot longer than the width.

The length of the other is 2 feet longer than the width. The larger rectangle has 4 more
square feet than the smaller. What is the width of the rectangles?

Answer 1

The width of the rectangles is 4.

Explanation:

Given that two rectangles have same width. So, let be the two rectangles
`R_(1)` and
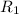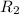`R_(2)` and width of rectangle is ‘x’. So, according to question, we have

Length of one rectangle ,
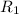`R_(1)` = x + 1

Length of other rectangle,
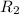`R_(2)` = x + 2

But we also know that,

`\text { Area of rectangle } = \text { Length } * \text { width }`

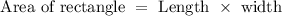
So, then the area for one rectangle,

`\text { Area of rectangle } R_(1) = x *(x+1)`

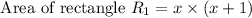
Similarly,

`\text { Area of rectangle } R_(2) = x *(x+2)`

So, according to question,

`\text {Area of rectangle } R_(2) = 4 * \text { Area of rectangle } R_(1)`

`x *(x+2) = 4+x *(x+1)`

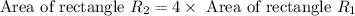
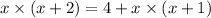
Now, by solving the above equation, we get

`x^(2)+2 x = 4+x^(2)+x`

`x = 4`

So, from the above equation, we found that width of the rectangle is 4.