Answer:
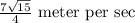
Explanation:
Let B represents the position of runner, A represents the position of the friend and C represents the position of centre of the circular track. ( shown below ),
We need to find :
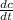
By the cosine law,

Differentiating with respect to t ( time ),
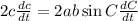

Now, by arc length formula,
Radius( say r ) × angle = arc length ( say l )
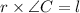
Differentiating w. r. t. t,
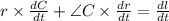
Here,
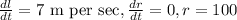
 ,
,
Now, again


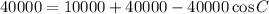
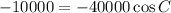
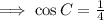
We know that,
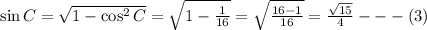
From equation (1), (2) and (3),
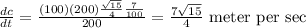
Hence, the distance between the friends changing with the rate of
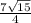 meter per sec.
meter per sec.