Question

What is the area of a sector with a central angle of 2π/9 radians and a diameter of 20.6 mm? use 3.14 for π and round your answer to the nearest hundredth. enter your answer as a decimal in the box.

this is just to help people:)

Answer 1

What is the area of a sector with a central angle of 2π9 radians and a diameter of 20.6 mm?

Use 3.14 for πand round your answer to the nearest hundredth.

Enter your answer as a decimal in the box.

The answer is

37.01 mm²

Explanation:

Answer 2

37.03 sq. mm.

Explanation:

A sector is "part" of a circle. The formula for area of a sector (in radians) is:

Area of sector =
`(1)/(2)r^2 \theta`

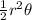
Where

r is the radius (half of diameter)

`\theta` is the central angle of the sector

In this problem, the diameter is given as 20.6, so radius would be:

Radius (r) = 20.6/2 = 10.3

The central angle is given as
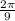`(2\pi)/(9)` radians

Now, we substitute and find the value for the area:

`A=(1)/(2)r^2 \theta\\A=(1)/(2)(10.3)^2 ((2\pi)/(9))\\A=(1)/(2)(106.09)((2(3.14))/(9))\\A=53.045*0.698\\A=37.03`

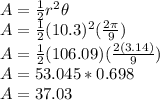
Thus,

Area of sector = 37.03 sq. mm.