Question

A 4.00 m-long steel cable is used to support a church chandelier. After the 226-kg chandelier is hung from the ceiling, the steel cable is lengthened by 3.00 mm. Calculate the diameter of the cable in millimeters. (The Young’s modulus for steel is ????????. ???????????????? × ???????????????????????????????? ????????/????????????????.)

Answer 1

4.22 mm

Step-by-step explanation:

E = Young’s modulus for steel = 210 GPa (generally)

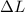`\Delta L` = Change in length = 3 mm

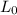`L_0` = Original length = 4 m

A = Area of cable

g = Acceleration due to gravity = 9.81 m/s²

r = Radius of cable

d = Diameter = 2r

m = Mass of chandelier = 226 kg

`\epsilon` = Longitudinal strain =
`(\Delta L)/(L_0)`

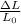
Uniaxial stress is given by

`\sigma=E\epsilon\\\Rightarrow \sigma=210* 10^9 (3* 10^(-3))/(4)\\\Rightarrow \sigma=157500000\ Pa`

`\sigma=(F)/(A)\\\Rightarrow \sigma=(mg)/(\pi r^2)\\\Rightarrow 157500000=(226* 9.81)/(\pi r^2)\\\Rightarrow r=\sqrt{(226* 9.81)/(157500000* \pi)}\\\Rightarrow r=0.00211\ m\\\Rightarrow d=2r\\\Rightarrow d=2* 2.11=4.22\ mm`

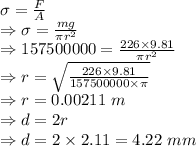
The diameter of the cable is 4.22 mm