Question

The mean annual tuition and fees for a sample of 12 private colleges was $36,800 with a standard deviation of $5000. A dotplot shows that it is reasonable to assume that the population is approximately normal. You wish to test whether the mean tuition and fees for private colleges is different from $33,700 Compute the value of the test statistic and state the number of degrees of freedom. A) 0.620; 12 degrees of freedom B) 0.620; 11 degrees of freedom C) 2.148; 12 degrees of freedom D) 2.148: 11 degrees of freedom

Answer 1

The value of the test statistic and the number of degrees of freedom is 2.148 and 11 respectively.

Explanation:

The mean annual tuition and fees for a sample of 12 private colleges was $36,800 with a standard deviation of $5000

`x= 36800\\s = 5000`

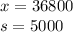
n = 12

Claim: You wish to test whether the mean tuition and fees for private colleges is different from $33,700

`H_0:\mu = 33700\\H_a:\mu \\eq 33700`

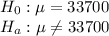
Since n < 30 and sample standard deviation is given so, we will use t test

Formula :
`t = (x-\mu)/((s)/(√(n)))`

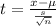
Substitute the values in the formula :

`t = (36800-33700)/((5000)/(√(12)))`

`t = 2.148`

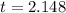
Degree of freedom = n-1 = 12-1 =11

So,. Option D is true

Hence the value of the test statistic and the number of degrees of freedom is 2.148 and 11 respectively.