Question

Write a quadratic function for each graph described.

The graph has x-intercept at -1 and 5/3, and the parabola pass through the point (5,40)

Answer 1

`y=2x^2-(4)/(3)x-(10)/(3)`

Explanation:

we know that

The roots of the quadratic function (x-intercepts) are

x=-1 and x=5/3

so

we can write the equation of the parabola as

`y=a(x+1)(x-(5)/(3))`

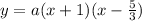
where

a is a coefficient

Remember that

The parabola pass through the point (5,40)

substitute the value of x and the value of y of the ordered pair in the quadratic equation and solve for a

x=5, y=40

`40=a(5+1)(5-(5)/(3))`

`40=a(6)((10)/(3))`

`40=20a\\a=2`

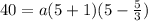
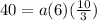
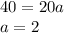
substitute

`y=2(x+1)(x-(5)/(3))`

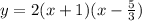
apply distributive property

`y=2(x^2-(5)/(3)x+x-(5)/(3))\\\\y=2(x^2-(2)/(3)x-(5)/(3))\\\\y=2x^2-(4)/(3)x-(10)/(3)`

see the attached figure to better understand the problem