Question

An alpha particle can be produced in certain radioactive decays of nuclei and consists of two protons and two neutrons. The particle has a charge of q = +2e and a mass of 4.00 u, where u is the atomic mass unit, with

1μ= 1.661×10^−27kg

Suppose an alpha particle travels in a circular path of radius 4.50 cm in a uniform magnetic field with B = 1.20 T. Calculate
(a) its speed.
(b) its period of revolution.
(c) its kinetic energy.
(d) the potential difference through which it would have to be accelerated to achieve this energy.

Answer 1

Step-by-step explanation:

charge, q = 2e = 2 x 1.6 x 10^-19 C = 3.2 x 10^-19 C

mass, m = 4 u = 4 x 1.661 x 10^-27 kg = 6.644 x 10^-27 kg

Radius, r = 4.5 cm = 0.045 m

Magnetic field, B = 1.20 T

(a) Let the speed is v.

`v=(Bqr)/(m)`

`v=(1.20* 3.2* 10^(-19)* 0.045)/(6.644* 10^(-27))`

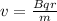
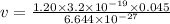
v = 2.6 x 10^6 m/s

(b) Let T be the period of revolution

`T=(2\pi r)/(v)`

`T=(2* 3.14* 0.045)/(2.6* 10^(6))`

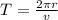
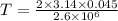
T = 1.09 x 10^-7 s

(c) The formula for the kinetic energy is

`K=(B^(2)* q^(2)* r^(2))/(2m)`

`K=(\left ( 1.20* 3.2 * 10^(-19)* 0.045 \right )^(2))/(2* 6.644* 10^(-27))`

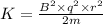
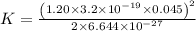
K = 2.25 x 10^-14 J

(d) Let the potential difference is V.

K = qV

`V = (K)/(q)`

`V= (2.25* 10^-14)/(3.2* 10^(-19))`

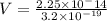
V = 70312.5 V