Answer:
The time period of revolution of the asteroid is 14.69 years.
Step-by-step explanation:
Given that,
Mass of asteroid
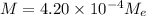
Distance
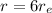
We need to calculate the velocity
Using relation centripetal force and gravitational force
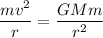
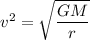
We need to calculate the time period of revolution of the asteroid
Using formula of time period
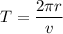
Put the value of v into the formula
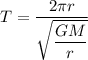 ...(I)
...(I)
We need to calculate the time period of revolution of the earth
Using formula of time period
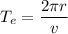
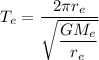 ....(II)
....(II)
From equation (I) and (II)
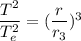

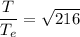
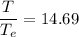
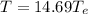
Hence, The time period of revolution of the asteroid is 14.69 years.