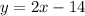Answer:
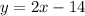
Explanation:
we know that
The equation of the line in slope intercept form is equal to

where
m is the slope
b is the y-intercept
In this problem we have
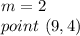
substitute the given in the equation
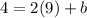
Solve for b
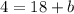
subtract 18 both sides
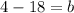
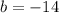
therefore
The linear equation in slope intercept form is equal to