Question

The Expression 4x^2-p(x)+7 leaves a remainder of -2 when divided by (x-3) find the value of p

A) 11
B)-2
C)15
D)40​

Answer 1

(c) For p = 15,
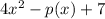`4x^2-p(x)+7` leaves a remainder of -2 when divided by (x-3).

Explanation:

Here, The dividend expression is
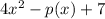`4x^2-p(x)+7` = E(x)

The Divisor = (x-3)

Remainder = -2

Now, by REMAINDER THEOREM:

Dividend = (Divisor x Quotient) + Remainder

If ( x -3 ) divides the given polynomial with a remainder -2.

⇒ x = 3 is a solution of given polynomial E(x) - (-2) =

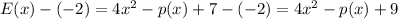`E(x)  - (-2)  = 4x^2-p(x)+7 -(-2)  = 4x^2-p(x)+9` = S(x)

Now, S(3) = 0

⇒
`4x^2-p(x)+9 = 4(3)^2 - p(3) + 9 = 0\\\implies 36 - 3p + 9 = 0\\\implies 45= 3p , \\or p  =15`

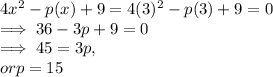
or, p =1 5

Hence, for p = 15,
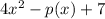`4x^2-p(x)+7` leaves a remainder of -2 when divided by (x-3).