Question

Answers and how to do them

Answer 1

1)121.5 sq.yards

2)157.92 m²

3)5.434 ft²

4)147.4513 cm²

5)147 cm²

6)56 in²

Explanation:

1) Area of shaded region= Area of rectangle-Area of triangle

Area of rectangle= Length*Breadth=18*9 sq.yards=162 sq.yards(length=18 yards and breadth=9 yards)

Area of triangle=
`(1)/(2)*Base*Height`=
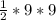`(1)/(2)*9*9`=40.5 sq.yards(base=9 yards and height= 9 yards)

Therefore,Area of shaded region=162-40.5=121.5 sq.yards

2) In the following figure,

Length of rectangle, l= 21 m

breadth of rectangle, b= 15 m

Radius of circles, r= 5 m

Area of rectangle=l*b=21*15=315 m²

Area of circle= π
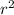`r^(2)`=π*
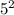`5^(2)`=78.54 m²

Therefore,Area of shaded region= Area of rectangle-2*Area of circle

=315-2*78.54=157.92 m²

3) In the following figure,

Radius of circle, r= 2 ft

Base of triangle, b= 6 ft

Height of triangle, h=6 ft

Area of circle= π
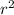`r^(2)`=π*
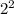`2^(2)`=12.566 ft²

Area of triangle=
`(1)/(2)*Base*Height`

=
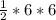`(1)/(2)*6*6`=18 ft²

Therefore,Area of shaded region= Area of triangle- Area of circle

= 18-12.566=5.434 ft²

4) In the following figure,

Radius of circle, r= 6 cm

Length of rectangle, l= 17 cm

breadth of rectangle, b= 2*r= 12 cm

Area of semi-circle= π
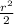`(r^(2))/(2)`=π*
`(6^(2))/(2)`

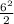
=56.5487 cm²

Area of rectangle=l*b=17*12=204 cm²

Therefore,Area of shaded region= Area of rectangle- Area of semi-circle

= 204-56.5487=147.4513 cm²

5) In the following figure,

Side of bigger square, a=14 cm

Side of smaller square, b=7 cm

Area of bigger square=
`a^(2)`=
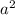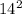`14^(2)`=196 cm²

Area of smaller square=
`b^(2)`=
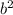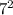`7^(2)`=49 cm²

Therefore,Area of shaded region= Area of bigger square- Area of smaller square

=196-49=147 cm²

6) In the following figure,

Length of rectangle, l= 10 in

breadth of rectangle, b= 8 in

Base of triangle, b= 8 in

Height of triangle, h=6 in

Area of rectangle=l*b=10*8=80 in²

Area of triangle=
`(1)/(2)*Base*Height`

=
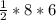`(1)/(2)*8*6`=24 in²

Therefore,Area of shaded region= Area of triangle- Area of circle

= 80-24=56 in²