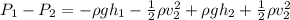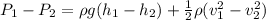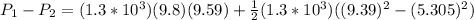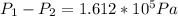Question

A liquid of density 1230 kg/m3 flows steadily through a pipe of varying diameter and height. At Location 1 along the pipe, the flow speed is 9.39 m/s and the pipe diameter d1 is 11.5 cm. At Location 2, the pipe diameter d2 is 15.3 cm. At Location 1, the pipe is Δy=9.59 m higher than it is at Location 2. Ignoring viscosity, calculate the difference ΔP between the fluid pressure at Location 2 and the fluid pressure at Location 1.

Answer 1

To develop this problem it is necessary to use the continuity equations and Bernoullie's theorem.

It is known from Bernoullie's theorem that

`P_1 + \rho gh_1+(1)/(2) \rho v_2^2 =P_2 + \rho gh_2+(1)/(2) \rho v_2^2`

Where

P = Pressure

g = Gravity

h= Height

v = Velocity

`\rho` = Density

On the other hand we have that the continuity equation is given by

`A_1v_1 = A_2 v_2`

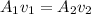
Where A is the Cross-sectional area and v the velocity.

For our values we know that

`A_1v_1 = A_2 v_2`

`((\pi d_1^2)/(4))v_1 =((\pi d_2^2)/(4))v_2`

`d_1^2v_1=d_2^2v_2`

`(11.5cm)^2(9.39)=(15.3)^2v_2`

`v_2 = 5.305m/s`

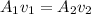
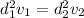
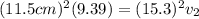
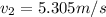
Using Bernoulli's expression we can now find the pressure difference,

`P_1 + \rho gh_1+(1)/(2) \rho v_2^2 =P_2 + \rho gh_2+(1)/(2) \rho v_2^2`

`P_1-P_2=-\rho gh_1-(1)/(2)\rho v_2^2 +\rho gh_2+(1)/(2) \rho v_2^2`

`P_1-P_2 = \rho g (h_1-h_2)+(1)/(2)\rho(v_1^2-v_2^2)`

`P_1-P_2 = (1.3*10^3)(9.8)(9.59)+(1)/(2)(1.3*10^3)((9.39)^2-(5.305)^2)`

`P_1-P_2 = 1.612*10^5Pa`