Question

Justify the last two steps of the proof Given ABCD is a parallelogram Prove ABC CDA

Answer 1

D. Reflexive Property of SSS

Answer 2

D

3. Reflexive Property of (Congruence) ≅

4. SSS (Side to Side to Side Congruence rule)

Explanation:

3. Any geometric figure compared to itself is congruent to itself so this is why:

`\overline{AC}\cong \overline{CA}\\\angle B\cong \angle B\\(...)`

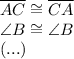
4. Since we have a parallelogram, therefore we can say:

`\overline{BC}\cong \overline{DA}\\\\\overline{BA}\cong \overline{DC}\\\\\overline{CA}\cong \overline{AC}\\`

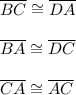
Both triangles ABC and CDA satisfy the side to side to side congruence, since their 3 sides are congruent.

So, It's D.

P.S.

Notice that the angle measure information is not included in the data above that's why we cannot say it is SAS congruence.