Question

Which statement can be used to prove that a given parallelogram is a rectangle? A) The opposite sides of the parallelogram are congruent. B) The diagonals of the parallelogram are congruent. C) The diagonals of the parallelogram bisect the angles. D) The opposite angles of the parallelogram are congruent.

Answer 1

B

Explanation:

I just took it

Answer 2

B) The diagonals of the parallelogram are congruent.

Explanation:

Since, If the diagonals of a parallelogram are equal in length, then is the parallelogram a rectangle.

For proving this statement.

Suppose PQRS is a parallelogram such that AC = BD,

In triangles ABC and BCD,

AB = CD, ( opposite sides of parallelogram )

AD = CB, ( opposite sides of parallelogram )

AC = BD ( given ),

By SSS congruence postulate,

`\triangle ABC\cong \triangle BCD`

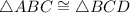
By CPCTC,

`m\angle ABC = m\angle BCD`

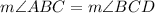
Now, Adjacent angles of a parallelogram are supplementary,

`\implies m\angle ABC + m\angle BCD = 180^(\circ)`

`\implies m\angle ABC + m\angle ABC = 180^(\circ)`

`\implies 2 m\angle ABC = 180^(\circ)`

`\implies m\angle ABC = 90^(\circ)`

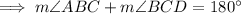
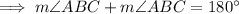
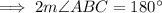
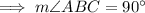
Since, opposite angles of a parallelogram are congruent,

`\implies m\angle ADC = 90^(\circ)`

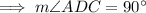
Similarly,

We can prove,

`m\angle DAB = m\angle BCD = 90^(\circ)`

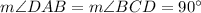
Hence, ABCD is a rectangle.

That is, OPTION B is correct.