Question

How do I solve this?

Answer 1

`t=(\pm√(dk))/(k)`

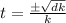
Explanation:

Given relation:

`d=k\ t^2`

We need to solve for
`t`

The given relation can be rearranged by isolating
`t` on one side.

Swapping the sides of the equation we have,

`k\ t^2=d`

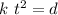
Dividing both sides by
`k` on order to cancel out
`k` on left side.

`(k\ t^2)/(k)=(d)/(k)`

`t^2=(d)/(k)`

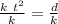
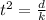
We have got an expression for
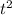`t^2` but we need to solve for
`t`

So, we take square root both sides to change
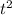`t^2` to
`t`

`√(t^2)=\sqrt{(d)/(k)}`

`t=\pm\sqrt{(d)/(k)}`

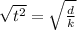
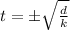
So, we have successfully isolated
`t` on left side.

But the expression we got is a fraction with a square root in the denominator. Thus we need to rationalize it to make it in simplest form.

The expression can be written by taking square root separately for numerator and denominator :

`t=\pm{(√(d))/(√(k))}`

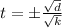
Multiplying the numerator and denominator by
`√(k)`

`t=\pm(√(d))/(√(k))*(√(k))/(√(k))`

`t=\pm(√(dk))/((√(k))^2)`

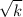
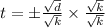
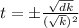
Square of a square root will remove the square root. Thus we have,

∴
`t=(\pm√(dk))/(k)`

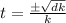
Thus we have successfully got the expression in the simplest form.