Question

Suppose m is in the line given by the equation 6x-3y=7, and suppose n is the line perpendicular to m and passing Nd through the point (6,2). If k is the line of slope 5 and y-intercept 1, what is the x-coordinate of the intersection of n and k? Express your answer in a common fraction.

Answer 1

To find the intersection point's x-coordinate, we used the slope-intercept form of the given lines, determined the perpendicular slope, and solved the system of equations. The x-coordinate where lines n and k intersect is 8/11.

Step-by-step explanation:

The problem requires us to determine the point of intersection between two lines, specifically the line n, which is perpendicular to line m and passes through the point (6,2), and the line k, which has a slope of 5 and a y-intercept of 1. To solve this, we first need to find the slope of line m to determine the slope of the perpendicular line n. The slope-intercept form of a straight line is given by y = mx + b, where m is the slope and b is the y-intercept.

For line m given by 6x - 3y = 7, we can rearrange it to y = 2x - 7/3. Thus, the slope of line m is 2, and the slope of the perpendicular line n is the negative reciprocal of this slope, which is -1/2. Line n passes through the point (6,2), so we can use the point-slope form to get its equation: y - 2 = (-1/2)(x - 6), simplifying to y = (-1/2)x + 5.

Next, we have the equation of line k as y = 5x + 1. To find the x-coordinate of their intersection, we set the two equations equal to each other: (-1/2)x + 5 = 5x + 1. Solving for x, we get 0 = (11/2)x - 4, which gives us x = 8/11. Therefore, the x-coordinate of the intersection of lines n and k is 8/11.

Answer 2

The x co-ordinate o intersection of line k and n is
`(8)/(11)`

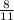
Step-by-step explanation:

Given as :

The equation of line m is 6 x - 3 y = 7

So, in the standard form , line equation is

y = a x + c , where a is the slope

So, 6 x - 3 y = 7 can be written as

3 y = 6 x - 7

or, y = 2 x -
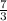`(7)/(3)` ........1

So, slope of this line = a = 2

Now, The line n is perpendicular to line m and passing through line ( 6 , 2 )

So, Slope of line n = b

For , perpendicular lines , products of slope = - 1

Or, a × b = -1

∴ b = -
`(1)/(a)`

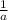
I.e b = -
`(1)/(2)`

So,equation of line n with slope b and passing through line ( 6 , 2 ) is

y -
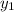`y_1` = b ( x -
`x_1` )

or, y - 2 = -
`(1)/(2)` ( x - 6 )

or, 2 × ( y - 2 ) = - 1 ( x - 6 )

or, 2 y - 4 = - x + 6

or, x + 2 y -10 = 0 ........2

Again, equation of line k with slope 5 and y intercept = 1

For y intercept , x coordinate = 0

y = c x + c

or, 1 = c× ( 0 ) + c

Or, c = 1

Or, equation of line k is

y = 5 x + 1 ..........3

Now intersection of line k and n is

put the value of y from eq 3 into eq 2

I.e x + 2 × ( 5 x + 1 )-10 = 0

Or, x + 10 x + 2 - 10 = 0

or, 11 x - 8 = 0

or 11 x = 8

∴ x =
`(8)/(11)`

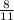
Hence The x co-ordinate o intersection of line k and n is
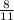`(8)/(11)` Answer