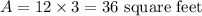The area of the deck is 36 square feet.
Solution:
Assume l is the length of the deck; w is its width, P is its perimeter and A is its area.
Given that length of a rectangular deck is 4 times its width
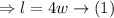
Perimeter of the deck is 30 ft
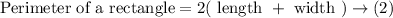
On substituting all the given values in (2) we get,
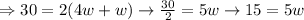
On dividing we get,
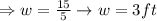
If w=3,
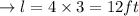
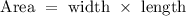
On substituting the values in the above formula we get,