Answer:
The rate at which the investment gets double is 7.776
Explanation:
Given as :
The principal investment = $ 5051
The time period of investment = 9 years
Let The rate of interest = R % compounded quarterly
The Amount gets double
So, From Compounded method
Amount = Principal ×
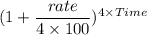
Or, 2 × P = P × ( 1 +

Or, 2 = ( 1 +

Or,
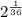 = 1 +
= 1 +
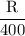
or, 1.01944 - 1 =
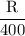
or, 0.01944 =
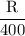
∴ R = 0.01944 × 400 = 7.776
Hence The rate at which the investment gets double is 7.776 Answer