The area of a triangle bounded by the y-axis is 8.49 square units
Solution:
Given that f(x) =
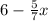
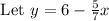
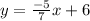
On comparing the above equation with slope intercept form.i.e
y = mx + c
where "m" is the slope and "c" is the y-intercept
So slope =
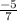
We know product of slopes of perpendicular line and given line is always -1
Slope of perpendicular line is given as:
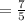
Equation of perpendicular line passing through origin (0, 0) is:
y = mx + c
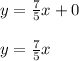
Intersecting point between the lines is:
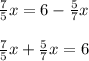
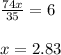
We know that
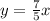
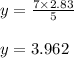
Point is (2.83, 3.962)
y intercept of line is
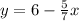
Put x = 0
Therefore y = 6
So the triangle is bounded by the points (0, 0) and (0, 6) and (2.83, 3.962)
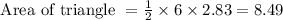
Thus area of triangle is 8.49 square units