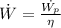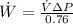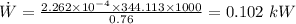Question

In large buildings, hot water in a water tank is circulated through a loop so that the user doesn’t have to wait for all the water in long piping to drain before hot water starts coming out. A certain recirculating loop involves 40-m-long, 1.2-cm-diameter cast iron pipes with six 90° threaded smooth bends and two fully open gate valves. If the average flow velocity through the loop is 2 m/s, determine the required power input for the recirculating pump. Take the average water temperature to be 60°C and the efficiency of the pump to be 76 percent. The density and dynamic viscosity of water at 60°C are rho = 983.3 kg/m3, μ = 0.467 × 10–3 kg/m·s. The roughness of cast iron pipes is 0.00026 m. The loss coefficient is KL = 0.9 for a threaded 90° smooth bend and KL = 0.2 for a fully open gate valve. (Round the final answer to three decimal paces.)

Answer 1

The power input is 0.102 kW

Solution:

As per the question:

Length of the loop, L = 40 m

Diameter of the loop, d = 1.2 cm

Velocity, v = 2 m/s

Loss coefficient of the threaded bends,
`K_(L, bend) = 0.9`

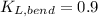
Loss coefficient of the valve,
`K_(L, valve) = 0.2`

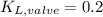
Dynamic viscosity of water,
`\mu = 0.467* 10^(- 3)\ kg/m.s`

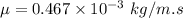
Density of water,
`\rho = 983.3\ kg/m^(3)`

Roughness of the pipe of cast iron,
`\epsilon = 0.00026\ m`

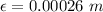
Efficiency of the pump,
`\eta = 0.76`

Now,

We calculate the volume flow rate as:

`\dot{V} = Av`

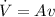
where

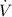`\dot{V}` = Volume rate flow

A = Area

v = velocity

`\dot{V} = (\pi)/(4)d^(2)* 2 = 2.262* 10^(- 4)\ m^(3)/s`

For this, Reynold's N. is given by:

`R_(e) = (\rho vd)/(\mu)`

`R_(e) = (983.3* 2* 0.012)/(0.467* 10^(- 3)) = 50533.62`

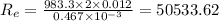
Since,
`R_(e)` > 4000, the flow is turbulent in nature.

Now,

With the help of the Colebrook eqn, we calculate the friction factor as:

`(1)/(√(f)) = - 2log[((\epsilon)/(d))/(3.7) + (2.51)/(R_(e)√(f))]`

`(1)/(√(f)) = - 2log[((0.00026)/(0.012))/(3.7) + (2.51)/(50533.62√(f))]`

f = 0.05075

Now,

To calculate the total head loss:

`H_(loss) = ((fL)/(d) + 6K_(L, bend) + 2K_(L, valve))\farc{v^(2)}{2g}`

`H_(loss) = ((0.05075* 40)/(0.012) + 6* 0.9 + 2* 0.2)\farc{2^(2)}{2* 9.8} = 35.71\ m`

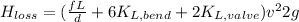
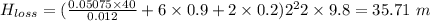
Now,

The drop in the pressure can be calculated as:

`\Delat P = \rho g H_(loss)`

`\Delat P = 983.3* 9.8* 35.71 = 344.113\ kN/m^(2)`

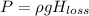
Now,

to calculate the input power:

`\dot{W} = \frac{\dot{W_(p)}}{\eta}`

`\dot{W} = \frac{\dot{V}\Delta P}{0.76}`

`\dot{W} = (2.262* 10^(- 4)* 344.113* 1000)/(0.76) = 0.102\ kW`