Question

A simple harmonic oscillator consists of a block of mass 4.10 kg attached to a spring of spring constant 240 N/m. When t = 1.70 s, the position and velocity of the block are x = 0.165 m and v = 3.780 m/s.

(a) What is the amplitude of the oscillations?

What were the (b) position and (c) velocity of the block at t = 0 s?

Answer 1

(a) the amplitude of the oscillations is 0.52 m

(b) position of the block at t = 0 s is - 0.06 m

(c) the velocity of the block at t = 0 s is 3.96 m/s

Step-by-step explanation:

given information:

m = 4.10 kg

k = 240 N/m

t = 1.70 s

x = 0.165 m

v = 3.780 m/s

(a) the amplitude of the oscillations

x(t) = A cos (ωt+φ)

v(t) = dx(t)/dt

= - ω A sin (ωt+φ)

ω =
`\sqrt{(k)/(m) }`

=
`\sqrt{(240)/(4.10) }`

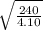
= 7.65 rad/s

v(t)/x(t) = - ω A sin (ωt+φ)/A cos (ωt+φ)

v(t)/x(t) = - ω sin (ωt+φ)/cos (ωt+φ)

v(t)/x(t) = - ω tan (ωt+φ)

(ωt+φ) =
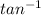`tan^(-1)` (-v/ωx)

=
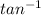`tan^(-1)` (-3.780/(7.65)(0.165))

= - 1.25

(ωt+φ) = - 1.25

φ = - 1.25 - ωt

= - 1.25 - (7.65 x 1.70)

= - 14.26

x(t) = A cos (ωt+φ)

A = x(t) / cos (ωt+φ)

= 0.165/cos(-1.25)

= 0.52 m

(b) position, at t=0

x(t) = A cos (ωt+φ)

x(0) = A cos (ω(0)+φ)

x(0) = A cos (φ)

= 0.52 cos (-14.26)

= - 0.06 m

(c) the velocity, at t=0

v(t) = - ω A sin (ωt+φ)

v(0) = - ω A sin (ω(0)+φ)

= - ω A sin (φ)

= - (7.65)(0.52) sin (-14.26)

= 3.96 m/s