Question

A manufacturer of chocolate chips would like to know whether its bag filling machine works correctly at the 420 gram setting. It is believed that the machine is underfilling the bags. A 24 bag sample had a mean of 414 grams with a standard deviation of 15. Assume the population is normally distributed. A level of significance of 0.1 will be used. Find the P-value of the test statistic.

Answer 1

P-value of the test statistic is 2.499

Step-by-step explanation:

given data:

size sample is 24

sample mean is 414 gm

standard deviation is 15

Null hypotheis is

`H_0: \mu = 420 gm`

`H_1 \mu< 420`

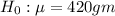
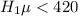
level of significance is 0.01

from test statics

`t = (\hat x - \mu)/((s)/(√(n)))`

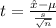
degree od freedom is = n -1

df = 24 -1 = 13

`t = (414 - 420)/((15)/(√(24)))`

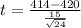
t = -1.959

from t table critical value of t at 0.1 significane level and 23 degree of freedom is 2.499