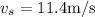Question

An unknown source plays a pitch of middle C (262 Hz). How fast would the sound wave from this source have to travel to raise

the pitch to C sharp (271 Hz)? Use 343 m/s as the speed of sound.
a. 2.8 m/s
c. 11.4 m/s
b. 15.6 m/s
d. 8.2 m/s

Answer 1

The sound travels at
`v_(s)=11.4 \mathrm{m} / \mathrm{s}`

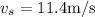
Option: c

Step-by-step explanation:

Unknown source plays of middle C (fs) = 262 Hz

The sound wave from this source have to travel to raise the pitch to C sharp is (fd) = 272 Hz

`\begin{array}{l}{velocity of sound in air(v)=343 \mathrm{m} / \mathrm{s}, f_{\mathrm{s}}=262 \mathrm{Hz}, f_{\mathrm{d}}=271 \mathrm{Hz}} \\ {velocity of receiver(v_{\mathrm{d}})=0 \mathrm{m} / \mathrm{s},velocity of source( v_{\mathrm{s}}) \text { is unknown }}\end{array}`

`\text { Speed of sound } \mathrm{V}_{\mathrm{S}}=343 \mathrm{m} / \mathrm{s}`

`f_{\mathrm{d}}=f_{\mathrm{s}}\left(\frac{v-v_{\mathrm{d}}}{v-v_{\mathrm{s}}}\right)`

`(f_(d))/(f_(s))=\left((v-v_(d))/(v-v_(s))\right)`

`\left(v-v_(s)\right)=(f_(s))/(f_(d))\left(v-v_(d)\right)`

`v_(s)=v-(f_(s))/(f_(d))\left(v-v_(d)\right)`

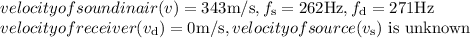
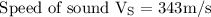
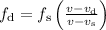
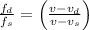
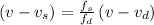
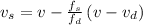
Substitute the given values in the formula,

`v_(s)=343+(262)/(271)(343-0)`

`v_(s)=343+0.966(343)`

`v_(s)=343-331.33`

`v_(s)=11.4 \mathrm{m} / \mathrm{s}`

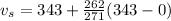
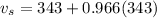
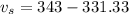
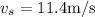
Therefore, The sound travels at
`v_(s)=11.4 \mathrm{m} / \mathrm{s}`