Question

Write the equation of the line that parallel to x = -3 and passes through the point (4, -7).

Answer 1

x = 4
This line goes through (4,-7) and is parallel to x=-3.

Answer 2

The equation of the line that parallel to x = -3 and passes through the point (4, -7) is y = -3x + 5

Solution:

The two forms of writing a point and slope in equation are point slope form and standard form.

The standard form of a line is in the form Ax + By = C where A is a positive integer, and B, and C are integers. The standard form of a line is just another way of writing the equation of a line.

The given point is (4,-7) and the slope is -3.

The slopes of parallel lines are always equal.

To write in standard form we will first write it in point slope form and then rearrange it into a standard from.

The equation of line in point slope form is given as:

`y-y_(1)=m\left(x-x_(1)\right)`

`\begin{array}{l}{y-(-7)=-3(x-4)} \\\\ {y+7=-3(x-4)} \\\\ {y+7=-3 x+12}\end{array}`

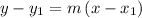
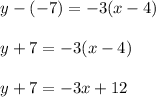
y = -3x + 5

Now, let us convert this equation to standard form

3x + y = 5

Thus the equation of line in point slope and standard form is found out