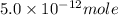Answer : The correct option is, (d)
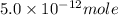
Explanation :
First we have to calculate the
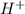 concentration.
concentration.
![pH=-\log [H^+]](https://img.qammunity.org/2020/formulas/chemistry/high-school/ipfjz05f4cfbguiwup37xvxa7furlbuapf.png)
![11.5=-\log [H^+]](https://img.qammunity.org/2020/formulas/chemistry/high-school/z1hbley6w323ynj0amv4c166v532zv7zeh.png)
![[H^+]=3.16* 10^(-12)M](https://img.qammunity.org/2020/formulas/chemistry/high-school/9hxg7odna3no8s67ssaybzij6x6n3hyg5y.png)
Now we have to calculate the
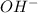 concentration.
concentration.
![[H^+][OH^-]=K_w](https://img.qammunity.org/2020/formulas/chemistry/college/zfeo9cpjxuenzlbyzisejh98ynub0dkhkr.png)
![3.16* 10^(-12)* [OH^-]=1.0* 10^(-14)](https://img.qammunity.org/2020/formulas/chemistry/high-school/gib6rcvkp2voinak73kl045dt7f0q2c7h2.png)
![[OH^-]=3.16* 10^(-3)M](https://img.qammunity.org/2020/formulas/chemistry/high-school/2ar3fo24g8hxvf4soy1rkj6up6qojlf4bd.png)
Now we have to calculate the molar solubility of
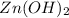 .
.
The balanced equilibrium reaction will be:
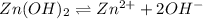
The expression for solubility constant for this reaction will be,
![K_(sp)=[Zn^(2+)][OH^-]^2](https://img.qammunity.org/2020/formulas/chemistry/high-school/1wkzny35evaw2yve1kk37divlycrr4fu4s.png)
Now put all the given values in this expression, we get:
![5.0* 10^(-17)=[Zn^(2+)]* (3.16* 10^(-3))^2](https://img.qammunity.org/2020/formulas/chemistry/high-school/eagjxed22zp0twhvzzudx4dv6t4evablqw.png)
![[Zn^(2+)]=5.0* 10^(-12)M](https://img.qammunity.org/2020/formulas/chemistry/high-school/sjlztbyph6as3dgxcj7k2g3506g11kcoix.png)
Therefore, the molar solubility of
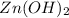 is,
is,